Does subgroup/wave size matter?
This week, I had a conversation with one of my coworkers about our subgroup/wave size heuristic and, in particular, whether or not control-flow divergence should be considered as part of the choice. This lead me down a fun path of looking into the statistics of control-flow divergence and the end result is somewhat surprising: Once you get above about an 8-wide subgroup, the subgroup size doesn’t matter.
Before I get into the details, let’s talk nomenclature. As you’re likely aware, GPUs often execute code in groups of 1 or more invocations. In D3D terminology, these are called waves. In Vulkan and OpenGL terminology, these are called subgroups. The two terms are interchangeable and, for the rest of this post, I’ll use the Vulkan/OpenGL conventions. Control-flow divergence
Before we dig into the statistics, let’s talk for a minute about control-flow divergence. This is mostly going to be a primer on SIMT execution and control-flow divergence in GPU architectures. If you’re already familiar, skip ahead to the next section.
Most modern GPUs use a Single Instruction Multiple Thread (SIMT) model. This means that the graphics programmer writes a shader which, for instance, colors a single pixel (fragment/pixel shader) but what the shader compiler produces is a program which colors, say, 32 pixels using a vector instruction set architecture (ISA). Each logical single-pixel execution of the shader is called an “invocation” while the physical vectorized execution of the shader which covers multiple pixels is called a wave or a subgroup. The size of the subgroup (number of pixels colored by a single hardware execution) varies depending on your architecture. On Intel, it can be 8, 16, or 32, on AMD, it’s 32 or 64 and, on Nvidia (if my knowledge is accurate), it’s always 32.
This conversion from logical single-pixel version of the shader to a physical multi-pixel version is often fairly straightforward. The GPU registers each hold N values and the instructions provided by the GPU ISA operate on N pieces of data at a time. If, for instance, you have an add in the logical shader, it’s converted to an add provided by the hardware ISA which adds N values. (This is, of course an over-simplification but it’s sufficient for now.) Sounds simple, right?
Where things get more complicated is when you have control-flow in your shader. Suppose you have an if statement with both then and else sections. What should we do when we hit that if statement? The if condition will be N Boolean values. If all of them are true or all of them are false, the answer is pretty simple: we do the then or the else respectively. If you have a mix of true and false values, we have to execute both sides. More specifically, the physical shader has to disable all of the invocations for which the condition is false and run the “then” side of the if statement. Once that’s complete, it has to re-enable those channels and disable the channels for which the condition is true and run the “else” side of the if statement. Once that’s complete, it re-enables all the channels and continues executing the code after the if statement.
When you start nesting if statements and throw loops into the mix, things get even more complicated. Loop continues have to disable all those channels until the next iteration of the loop, loop breaks have to disable all those channels until the loop is entirely complete, and the physical shader has to figure out when there are no channels left and complete the loop. This makes for some fun and interesting challenges for GPU compiler developers. Also, believe it or not, everything I just said is a massive over-simplification. :-)
The point which most graphics developers need to understand and what’s important for this blog post is that the physical shader has to execute every path taken by any invocation in the subgroup. For loops, this means that it has to execute the loop enough times for the worst case in the subgroup. This means that if you have the same work in both the then and else sides of an if statement, that work may get executed twice rather than once and you may be better off pulling it outside the if. It also means that if you have something particularly expensive and you put it inside an if statement, that doesn’t mean that you only pay for it when needed, it means you pay for it whenever any invocation in the subgroup needs it.
Fun with statistics
At the end of the last section, I said that one of the problems with the SIMT model used by GPUs is that they end up having worst-case performance for the subgroup. Every path through the shader which has to be executed for any invocation in the subgroup has to be taken by the shader as a whole. The question that naturally arises is, “does a larger subgroup size make this worst-case behavior worse?” Clearly, the naive answer is, “yes”. If you have a subgroup size of 1, you only execute exactly what’s needed and if you have a subgroup size of 2 or more, you end up hitting this worst-case behavior. If you go higher, the bad cases should be more likely, right? Yes, but maybe not quite like you think.
This is one of those cases where statistics can be surprising. Let’s say you have an if statement with a boolean condition b. That condition is actually a vector (b1, b2, b3, …, bN) and if any two of those vector elements differ, we path the cost of both paths. Assuming that the conditions are independent identically distributed (IID) random variables, the probability of entire vector being true is P(all(bi = true) = P(b1 = true) * P(b2 = true) * … * P(bN = true) = P(bi = true)^N where N is the size of the subgroup. Therefore, the probability of having uniform control-flow is P(bi = true)^N + P(bi = false)^N. The probability of non-uniform control-flow, on the other hand, is 1 - P(bi = true)^N - P(bi = false)^N.
Before we go further with the math, let’s put some solid numbers on it. Let’s say we have a subgroup size of 8 (the smallest Intel can do) and let’s say that our input data is a series of coin flips where bi is “flip i was heads”. Then P(bi = true) = P(bi = false) = 1/2. Using the math in the previous paragraph, P(uniform) = P(bi = true)^8 + P(bi = false)^8 = 1/128. This means that the there is only a 1:128 chance that that you’ll get uniform control-flow and a 127:128 chance that you’ll end up taking both paths of your if statement. If we increase the subgroup size to 64 (the maximum among AMD, Intel, and Nvidia), you get a 1:2^63 chance of having uniform control-flow and a (263-1):263 chance of executing both halves. If we assume that the shader takes T time units when control-flow is uniform and 2T time units when control-flow is non-uniform, then the amortized cost of the shader for a subgroup size of 8 is 1/128 * T + 127/128 * 2T = 255/128 T and, by a similar calculation, the cost of a shader with a subgroup size of 64 is (2^64 - 1)/2^63. Both of those are within rounding error of 2T and the added cost of using the massively wider subgroup size is less than 1%. Playing with the statistics a bit, the following chart shows the probability of divergence vs. the subgroup size for various choices of P(bi = true):
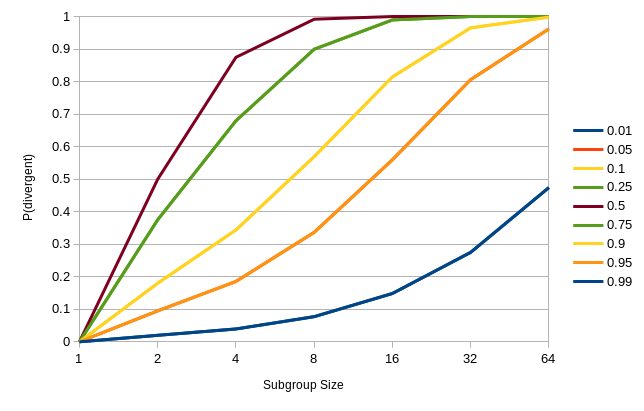
One thing to immediately notice is that because we’re only concerned about the probability of divergence and not of the two halves of the if independently, the graph is symmetric (p=0.9 and p=0.1 are the same). Second, and the point I was trying to make with all of the math above, is that until your probability gets pretty extreme (> 90%) the probability of divergence is reasonably high at any subgroup size. From the perspective of a compiler with no knowledge of the input data, we have to assume every if condition is a 50/50 chance at which point we can basically assume it will always diverge.
Instead of only considering divergence, let’s take a quick look at another case. Let’s say that the you have a one-sided if statement (no else) that is expensive but rare. To put numbers on it, let’s say the probability of the if statement being taken is 1/16 for any given invocation. Then P(taken) = P(any(bi = true)) = 1 - P(all(bi = false)) = 1 - P(bi = false)^N = 1 - (15/16)^N. This works out to about 0.4 for a subgroup size of 8, 0.65 for 16, 0.87 for 32, and 0.98 for 64. The following chart shows what happens if we play around with the probabilities of our if condition a bit more:
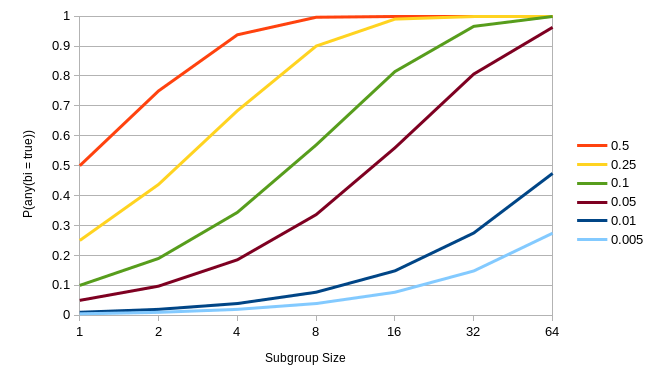
As we saw with the earlier divergence plot, even events with a fairly low probability (10%) are fairly likely to happen even with a subgroup size of 8 (57%) and are even more likely the higher the subgroup size goes. Again, from the perspective of a compiler with no knowledge of the data trying to make heuristic decisions, it looks like “ifs always happen” is a reasonable assumption. However, if we have something expensive like a texture instruction that we can easily move into an if statement, we may as well. There’s no guarantees but if the probability of that if statement is low enough, we might be able to avoid it at least some of the time.
Statistical independence
A keen statistical eye may have caught a subtle statement I made very early on in the previous section:
Assuming that the conditions are independent identically distributed (IID) random variables…
While less statistically minded readers may have glossed over this as meaningless math jargon, it’s actually very important assumption. Let’s take a minute to break it down. A random variable in statistics is just an event. In our case, it’s something like “the if condition was true”. To say that a set of random variables is identically distributed means that they have the same underlying probabilities. Two coin tosses, for instance, are identically distributed while the distribution of “coin came up heads” and “die came up 6” are very different. When combining random variables, we have to be careful to ensure that we’re not mixing apples and oranges. All of the analysis above was looking at the evaluation of a boolean in the same if condition but across different subgroup invocations. These should be identically distributed.
The remaining word that’s of critical importance in the IID assumption is “independent”. Two random variables are said to be independent if they have no effect on one another or, to be more precise, knowing the value of one tells you nothing whatsoever about the value of the other. Random variables which are not dependent are said to be “correlated”. One example of random variables which are very much not independent would be housing prices in a neighborhood because the first thing home appraisers look at to determine the value of a house is the value of other houses in the same area that have sold recently. In my computations above, I used the rule that P(X and Y) = P(X) * P(Y) but this only holds if X and Y are independent random variables. If they’re dependent, the statistics look very different. This raises an obvious question: Are if conditions statistically independent across a subgroup? The short answer is “no”.
How does this correlation and lack of independence (those are the same) affect the statistics? If two events X and Y are negatively correlated then P(X and Y) < P(X) * P(Y) and if two events are positively correlated then P(X and Y) > P(X) * P(Y). When it comes to if conditions across a subgroup, most correlations that matter are positive. Going back to our statistics calculations, the probability of if condition diverging is 1 - P(all(bi = true)) - P(all(bi = false)) and P(all(bi = true)) = P(b1 = true and b2 = true and… bN = true). So, if the data is positively correlated, we get P(all(bi = true)) > P(bi = true)^N and P(divergent) = 1 - P(all(bi = true)) - P(all(bi = false)) < 1 - P(bi = true)^N - P(bi = false)^N. So correlation for us typically reduces the probability of divergence. This is a good thing because divergence is expensive. How much does it reduce the probability of divergence? That’s hard to tell without deep knowledge of the data but there are a few easy cases to analyze.
One particular example of dependence that comes up all the time is uniform values. Many values passed into a shader are the same for all invocations within a draw call or for all pixels within a group of primitives. Sometimes the compiler is privy to this information (if it comes from a uniform or constant buffer, for instance) but often it isn’t. It’s fairly common for apps to pass some bit of data as a vertex attribute which, even though it’s specified per-vertex, is actually the same for all of them. If a bit of data is uniform (even if the compiler doesn’t know it is), then any if conditions based on that data (or from a calculation using entirely uniform values) will be the same. From a statics perspective, this means that P(all(bi = true)) + P(all(bi = false)) = 1 and P(divergent) = 0. From a shader execution perspective, this means that it will never diverge no matter the probability of the condition because our entire wave will evaluate the same value.
What about non-uniform values such as vertex positions, texture coordinates, and computed values? In your average vertex, geometry, or tessellation shader, these are likely to be effectively independent. Yes, there are patterns in the data such as common edges and some triangles being closer to others. However, there is typically a lot of vertex data and the way that vertices get mapped to subgroups is random enough that these correlations between vertices aren’t likely to show up in any meaningful way. (I don’t have a mathematical proof for this off-hand.) When they’re independent, all the statistics we did in the previous section apply directly.
With pixel/fragment shaders, on the other hand, things get more interesting. Most GPUs rasterize pixels in groups of 2x2 pixels where each 2x2 pixel group comes from the same primitive. Each subgroup is made up of a series of these 2x2 pixel groups so, if the subgroup size is 16, it’s actually 4 groups of 2x2 pixels each. Within a given 2x2 pixel group, the chances of a given value within the shader being the same for each pixel in that 2x2 group is quite high. If we have a condition which is the same within each 2x2 pixel group then, from the perspective of divergence analysis, the subgroup size is effectively divided by 4. As you can see in the earlier charts (for which I conveniently provided small subgroup sizes), the difference between a subgroup size of 2 and 4 is typically much larger than between 8 and 16.
Another common source of correlation in fragment shader data comes from the primitives themselves. Even if they may be different between triangles, values are often the same or very tightly correlated between pixels in the same triangle. This is sort of a super-set of the 2x2 pixel group issue we just covered. This is important because this is a type of correlation that hardware has the ability to encourage. For instance, hardware can choose to dispatch subgroups such that each subgroup only contains pixels from the same primitive. Even if the hardware typically mixes primitives within the same subgroup, it can attempt to group things together to increase data correlation and reduce divergence.
Why bother with subgroups?
All this discussion of control-flow divergence might leave you wondering why we bother with subgroups at all. Clearly, they’re a pain. They definitely are. Oh, you have no idea…
But they also bring some significant advantages in that the parallelism allows us to get better throughput out of the hardware. One obvious way this helps is that we can spend less hardware on instruction decoding (we only have to decode once for the whole wave) and put those gates into more floating-point arithmetic units. Also, most processors are pipelined and, while they can start processing a new instruction each cycle, it takes several cycles before an instruction makes its way from the start of the pipeline to the end and its result can be used in a subsequent instruction. If you have a lot of back-to-back dependent calculations in the shader, you can end up with lots of stalls where an instruction goes into the pipeline and the next instruction depends on its value and so you have to wait 10ish cycles until for the previous instruction to complete. On Intel, each SIMD32 instruction is actually four SIMD8 instructions that pipeline very nicely and so it’s easier to keep the ALU busy.
Ok, so wider subgroups are good, right? Go as wide as you can! Well, yes and no. Generally, there’s a point of diminishing returns. Is one instruction decoder per 32 invocations of ALU really that much more hardware than one per 64 invocations? Probalby not. Generally, the subgroup size is determined based on what’s required to keep the underlying floating-point arithmetic hardware full. If you have 4 ALUs per execution unit and a pipeline depth of 10 cycles, then an 8-wide subgroup is going to have trouble keeping the ALU full. A 32-wide subgroup, on the other hand, will keep it 80% full even with back-to-back dependent instructions so going 64-wide is pointless.
On Intel GPU hardware, there are additional considerations. While most GPUs have a fixed subgroup size, ours is configurable and the subgroup size is chosen by the compiler. What’s less flexible for us is our register file. We have a fixed register file size of 4KB regardless of the subgroup size so, depending on how many temporary values your shader uses, it may be difficult to compile it 16 or 32-wide and still fit everything in registers. While wider programs generally yield better parallelism, the additional register pressure can easily negate any parallelism benefits.
There are also other issues such as cache utilization and thrashing but those are way out of scope for this blog post…
What does this all mean?
This topic came up this week in the context of tuning our subgroup size heuristic in the Intel Linux 3D drivers. In particular, how should that heuristic reason about control-flow and divergence? Are wider programs more expensive because they have the potential to diverge more?
After all the analysis above, the conclusion I’ve come to is that any given if condition falls roughly into one of three categories:
Effectively uniform. It never (or very rarely ever) diverges. In this case, there is no difference between subgroup sizes because it never diverges.
Random. Since we have no knowledge about the data in the compiler, we have to assume that random if conditions are basically a coin flip every time. Even with our smallest subgroup size of 8, this means it’s going to diverge with a probability of 99.6%. Even if you assume 2x2 subspans in fragment shaders are strongly correlated, divergence is still likely with a probability of 75% for SIMD8 shaders, 94% for SIMD16, and 99.6% for SIMD32.
Random but very one-sided. These conditions are the type where we can actually get serious statistical differences between the different subgroup sizes. Unfortunately, we have no way of knowing when an if condition will be in this category so it’s impossible to make heuristic decisions based on it.
Where does that leave our heuristic? The only interesting case in the above three is random data in fragment shaders. In our experience, the increased parallelism going from SIMD8 to SIMD16 is huge so it probably makes up for the increased divergence. The parallelism increase from SIMD16 to SIMD32 isn’t huge but the change in the probability of a random if diverging is pretty small (94% vs. 99.6%) so, all other things being equal, it’s probably better to go SIMD32.

